定義

分析一個解決問題的方法（演算法）是不是好的方法，需要一個判斷的基準。而時間複雜度，就是用來計算這個方法的基準。

1. 表示的方法寫成「 O() 」，描述演算法在輸入n個東西時，執行次數與 n 的關係
2. 在輸入的東西 n 無比大的時候，好的演算法可以省下很多時間
3. 演算法的速度不是以秒數來計算，而是以步驟次數來計算
4. 實務上我們只會紀錄最高次方的那一項，並忽略其他所有係數
   • 通常我們會用函數來表達時間 f(n) = 2n² + n + 3
   • 因為函數中，除了最高次方的項目以外（低階項，以及最高次方係數），對函數的影響相對於最高次方的項目，影響很小，所以就忽略不計，我們會把他表達成他運行的時間是 n²，我們表示成 O(n²)
5. 關心的重點是，隨著輸入大小的增長，運行時間會以怎樣的速度擴張

常見的幾個時間複雜度分析

1. O(1)
2. O(n)
3. O(n²)
4. O(log n)

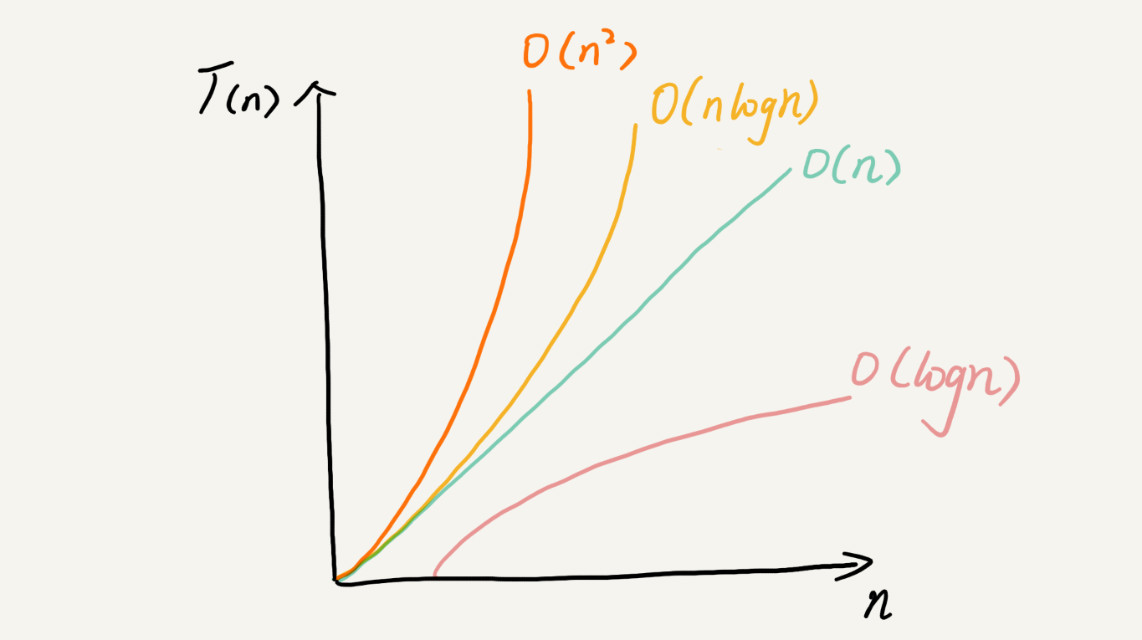
我們來深入解釋一下，讓大家對時間複雜度更有感覺

O(1)

O(1) 也就是最低的時間複雜度，也就是說耗時，與輸入的資料量大小無關，也就是說資料無論增加多少倍，消耗的時間不變

1
2
3
4
5

func getNum(target int)int{
  var arr = []int{1,2,3,4,5}
  // 想要從陣列中拿取某個位置的值，無論陣列多大都是 O(1)
  return arr[2]
}

O(n)

演算法的時間複雜度，隨著資料量大多少，執行次數就增加多少

1
2
3
4
5
6
7

func printNum(target int){
  var arr = []int{1,2,3,4,5}
  // 陣列多加一個值，迴圈就會多跑一次
  for _, value := range arr{
        fmt.Println(value)
  }
}

O(n²)

O(n²)，表示資料量增大 n 倍時，耗時增大 n² 倍

例如：泡沫排序法，對於 n 個數排序，需要掃描 n * n次

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

func bubble_sort(input int){
  stopFlag := true
  for stopFlag{
    stopFlag = false
    for item :=0; item <len(input)-1;item++{
        if input[item] > input[item -1]{
                input[item], input[item-1] = input[item-1], input[item]
                stopFlag = true
        }
    }          
  }
}

O(log n)

log n 其實是比較難直覺上理解的，我們來講一個故事，來大概理解一下log n 是什麼感覺好了

傳說在丹尼爾王國裡面，有一個發明家叫做酷比，而酷比發明了 “象棋”，使得丹尼爾國王非常開心， 他決定要重重的賞賜酷比。酷比說：我不要陛下的重賞，我只要陛下在我的旗盤上賞我一些米粒就可以了！ 在第一個格子裡放一粒米，在第二個格子放兩粒，在地三個格子放四粒，第四個格子放八粒，依此類推，放滿64格就好了。 丹尼爾國王就說：小事，來人，上米！結果還沒放到20格，一袋米就用光了，一袋又一袋的米被扛到國王面前，但是要放到格子裡的米的數量卻非快的增長著，國王很快就發現了，即使拿出全國的米粒，也很難兌現對酷比的諾言！

當資料增大 n 倍時，耗時只增加 log n倍，(這裡的資料是以2為底，當資料增大256倍時，時間只成長了8倍) 「忘記 log 是啥的同學，我們回憶一下 log n = x 的意思是， n = 2^x ，舉例說明: n = 4 ，4 = 2²，程式兩個步驟就完成了，n = 16 時，程式會在 4 個步驟完成（16 = 2⁴）」

例如：二元搜尋法，每找一次排除一半的可能，256 個資料只要找8 次即可

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

// 前提是輸入的資料已經排序完成，返回該數字所在位置，沒有就返回-1
func binary_search(input []int,target int)int{
  lower := 0
  upper := len(input) -1
  var mid int
  for{
    mid = (uower + upper)/2
    if input[mid] == target {
       return mid
    }
    if input[mid]< target {
        lower = mid + 1
    } else{
        upper = mid -1
    }
  }
  return -1
}

小結

在這篇文章中，了解了時間複雜度，而在接下來的文章中，我們會開始認識「排序法」，以及在更進階的例子。 寫到這裡希望可以清楚且簡單的描述，時間複雜度，以及對時間複雜度的感覺